算法基础

算法可视化：

数据结构和算法动态可视化 (Chinese) - VisuAlgo

Data Structure Visualization (usfca.edu)

数据结构和算法：（图文解析）Hello 算法 (hello-algo.com) （github项目源码地址：krahets/hello-algo: 《Hello 算法》：动画图解、一键运行的数据结构与算法教程，支持 Java, C++, Python, Go, JS, TS, C#, Swift, Rust, Dart, Zig 等语言。 (github.com)）

c++中没有split库函数，我们可以自己封装一个

这里我们会用到一个c++的库函数strtok()

函数原型	char * strtok(char *s, const char *delim)
函数功能	分解字符串为一组字符串， s为要分解的字符串，delim为分隔字符串
描述	strtok()用来将字符串分隔成一个个小片段，参数s指向将要被分隔的字符串，参数delim则为分隔字符串，当strtok()在参数s的字符串中发现到参数delim的分隔符时，则会将该字符串改为 ‘\0’ 字符，在第一次调用时，strtok()必须给予参数s字符串，往后的调用则将参数s设置成NULL。每次调用成功则返回被分隔 片段的指针。

vector<string> split(const string& str, const string& delim) {
    //str:需要处理的字符串 delim:分隔符
    vector<string> res;
    if("" == str) return res;
    //先将要切割的字符串从string类型转换为char*类型
    char * strs = new char[str.length() + 1];//这里str.length()+1是因为还要加上字符串的结束符 '\0'
    strcpy(strs, str.c_str());//将str字符串从string转换为char*型字符串，然后拷贝到strs中
    char * d = new char[delim.length() + 1];//分割符不一定是一个字符，在输入分隔符的时候可能是一个字符串
    strcpy(d, delim.c_str());
    
    char * p = strtok(strs, d);
    while(p) {
        string s = p; //分割得到的字符串转换为string类型
        res.push_back(s);//存入结果数组
        p = strtok(NULL, d);
    }
    return res;
}

排序算法：

直接插入排序：(稳定)

时间复杂度：O(n^2)

存放待排序序列的数组的第一个位置不存储数据，该位置作为哨兵位，暂存我们正在处理的那个元素的值

#include<iostream>
using namespace std;
int main()
{
	int k; 
	int *L;
	int listsize,i,j;
	cout<<"请输入listsize的值=";
	cin>>listsize;
	L=new int[listsize+1];
	for(i=1;i<=listsize;i++)//结果为递增排序 
		cin>>L[i];//待排列的数据在数组中从数组下标为1的位置开始存储 
		for(i=2;i<=listsize;i++) {
			if(L[i]<L[i-1]){//如果需要处理的元素小于其前一个元素，不符合递增规定 
				L[0]=L[i];//L[0]为哨兵位，将需要处理的元素先放到L[0]这个位置上 
				j=i;//由于后面要从需要处理的位置往前查询，找出该元素因该插入的位置需要更改i的值，所以要用j代替i 
				while(L[j - 1] > L[0]) {//如果某个位置其前一个元素的值小于等于L[0]的值，找到了插入的位置 
					L[j] = L[j - 1];
					j--;
				} 
				L[j] = L[0];//插入元素 
			}	
			for(k=1;k<=listsize;k++)
				cout<<L[k]<<" ";
				cout<<endl;	
		}
		cout << "最终的结果："; 
		for(i=1;i<=listsize;i++)
		cout<<L[i]<<" ";
		return 0;
 } 

折半插入排序：（稳定）

时间复杂度：O(n^2)

这里我们用到了二分查找（折半查找）,来确定需要插入的位置。

注意：二分查找只适用于有序序列的查找，而且对于升序序列和降序序列的二分查找函数的写法是不一样的

这里我们使用的是升序序列的二分查找

存放待排序序列的数组的第一个位置不存储数据，该位置作为哨兵位，暂存我们正在处理的那个元素的值

#include<iostream>
#include<vector>
using namespace std;
void display(vector<int> v) {
	for(int i = 1; i < v.size(); i++) {
		cout << v[i] << " ";
	}cout << endl;
}
void Binary_Insertion_Sort(vector<int>& v) {
	int low, high;
	for(int i = 2; i < v.size(); i++) {
		if(v[i] < v[i - 1]) {
			v[0] = v[i];
			low = 1; high = i - 1;
			while(low <= high) {
				int mid = (low + high) / 2;
				if(v[0] > v[mid]) {
					low = mid + 1;
				}else {
					high = mid - 1;
				}  
			}
			for(int j = i - 1; j >= low; --j) {
				v[j + 1] = v[j];
			}
			v[low] = v[0];
		}
		cout << "第" << i - 1 <<"趟排序：";
		display(v); 
	}
}
int main() {
	int n;
	cout << "请输入元素的个数：";
	cin >> n;
	vector<int> v(n + 1);
	cout << "请输入待排序序列：";
	for(int i = 1; i <= n; i++) {
		cin >> v[i];
	} 
	Binary_Insertion_Sort(v);
}

希尔排序：（不稳定）

时间复杂度：O(n^1.3)

存放待排序序列的数组的第一个位置不存储数据，该位置作为哨兵位，暂存我们正在处理的那个元素的值

#include<iostream>
#include<vector>
using namespace std;
void display(vector<int> v) {
	for(int i = 1; i < v.size(); i++) {
		cout << v[i] << " ";
	}cout << endl;
}
void ShellSort(vector<int>& v, int n) {
	int dk, i, j;int cnt = 1; 
	for(dk = n/2; dk >= 1; dk /= 2) {
		for(i = 1 + dk; i <= n; i++) {
			if(v[i] < v[i - dk]) {
				v[0] = v[i];
				j = i;
				while(j - dk >= 0 && v[j - dk] > v[0]) {
					v[j] = v[j - dk];
					j -= dk;
				}
				v[j] = v[0];
			}
		}
		cout << "第" << cnt++ <<"趟排序：";
		display(v); 
	}
}
int main() {
	int n;
    cout << "请输入元素的个数：";
	cin >> n;
	vector<int> v(n + 1);
    cout << "请输入待排序序列：";
	for(int i = 1; i <= n; i++)
		cin >> v[i];
	ShellSort(v, n);
	
	return 0;
}

冒泡排序：（稳定）

时间复杂度：O(n^2)

void bubble(vector<int> &v) {
    int temp;
    int n = v.size();
    for(int i = 1; i < n; i++) {
        bool flag = false;
        for(int j = 0; j < n - i; j++) {
            if(v[j] > v[j + 1]) {
                temp = v[j];
                v[j] = v[j + 1];
                v[j + 1] = temp;
                flag = true;
            }
        }
        if(flag == false) {//如果本趟遍历后没有发生交换，说明表已经有序
            return;
        }
    }
}

快速排序：（不稳定）（最常使用，效率相对较好）

时间复杂度 = O(n * 递归层数) = O(nlog2n)

空间复杂度 = O(递归层数) = O(log2n)

递归层数可以转化为二叉树的高度（log2n ~ n）(最高 ~ 最矮) n为结点个数

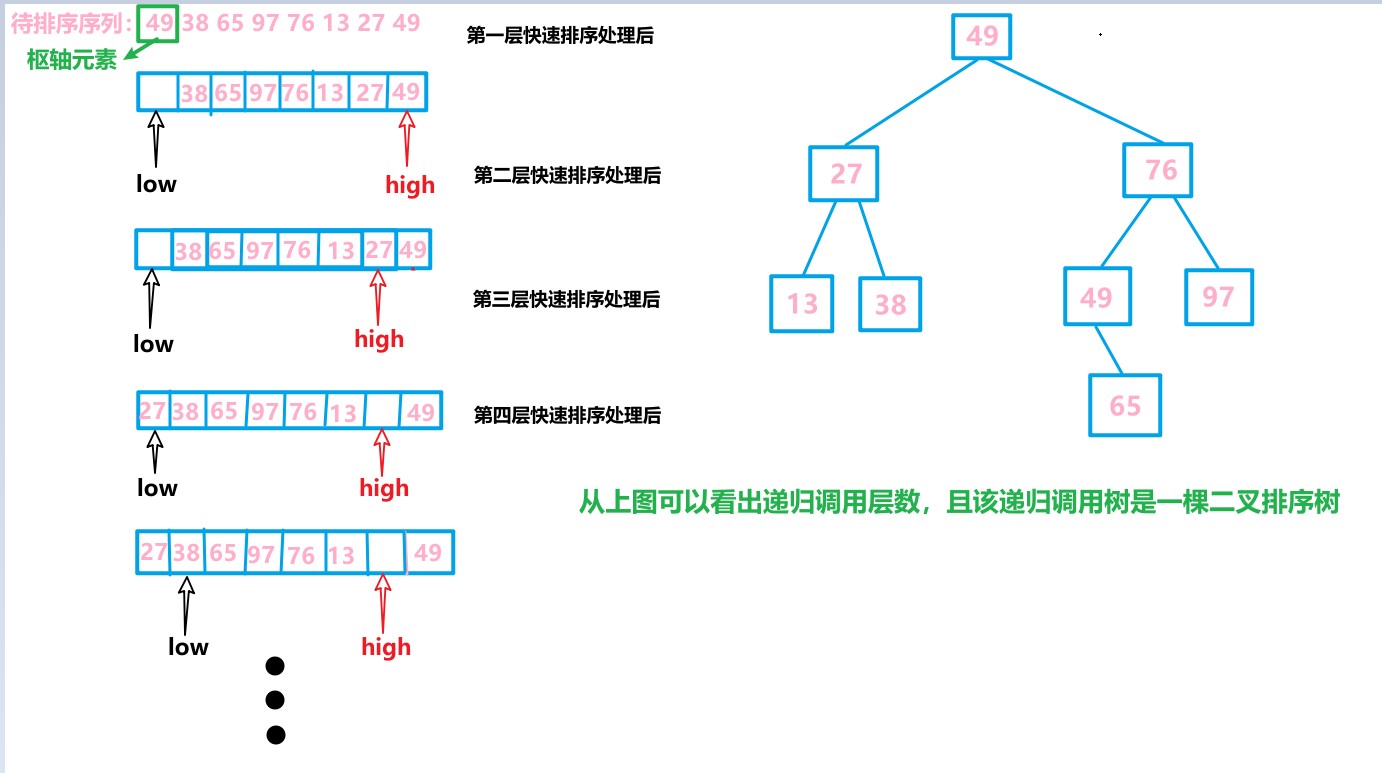
快速排序在处理有序序列的排序时效率是最低的。若每一次选中的枢轴元素将待排序序列划分为很不均匀的两个部分，则会导致递归深度增加，算法效率变低

快速排序算法优化思路：尽量选择可以把数据 中分的 枢轴元素

例如：1、选头、中、尾三个位置的元素，取中间值作为枢轴元素

​ 2、随机选一个元素作为枢轴元素

算法思路：先确定一个枢轴元素，将这个位置的值用一个变量记录下来，然后用两个指针low和high分别指向待排序序列的头和尾，先从high指针往前判断，如果high指针所指向的元素小于枢轴元素，那么就将该元素放到low指针所指向的位置，然后再从low指针往后判断，如果low指针所指向的元素大于枢轴元素，那么就将该元素放到high指针所指向的位置，这样就能使得low指针左边的元素都小于枢轴元素，high指针右边的元素都大于枢轴元素；然后依次循环往复，直到low==high时，即找到了枢轴元素应该放入的位置。

#include<iostream>
#include<vector>
using namespace std;
int partition(vector<int> &v, int low, int high) {
	int pivot = v[low];//将第一个元素作为枢轴元素
	while(low < high) {
		while(low < high && v[high] >= pivot) { //先处理high指针 
			--high;
		}v[low] = v[high];
		while(low < high && v[low] <= pivot) { //处理low指针 
			++low;
		}v[high] = v[low];
	}//循环结束后low==high
	v[low] = pivot;
	return low; 
}
void QuickSort(vector<int> &v, int low, int high) {
	if(low < high) {
		int pivotPos = partition(v, low, high);
		QuickSort(v, low, pivotPos - 1);//递归处理low ~ pivotPos - 1的序列 
		QuickSort(v, pivotPos + 1, high);//递归处理pivotPos - 1 ~ high的序列
	}
}
int main() {
	int n;
	cout << "请输入待排序序列中元素的个数：";
	cin >> n;
	vector<int> v(n);
	cout << "请输入待排序序列：";
	for(int i = 0; i < n; i++) {
		cin >> v[i];
	} 
	QuickSort(v, 0, n - 1);
	for(int i = 0; i < n; i++) {
		cout << v[i] << " ";
	}
	return 0;
}

简单选择排序：（不稳定）

时间复杂度：O(n^2)

void SelectSort(vector<int> v) {
    for(k = 0; k < n - 1; k++) {
		index = k;
		for(i = k + 1; i < n; i++)
			if(a[i] < a[index])
				index = i;
		temp = a[index];
		a[index] = a[k];
		a[k] = temp;
	}
}

堆排序：（不稳定）

考研考察频率比较高

时间复杂度：O(nlog2n)

空间复杂度：O(1)

建堆时间：O(n)

建堆：( O(n) )

思路：把所有非终端结点都检查一遍，是否满足大根/小根堆的要求，如果不满足，则进行调整

可以将堆视为一棵完全二叉树

在顺序存储的完全二叉树中，非终端结点编号 i <= ⌊ n/2 ⌋

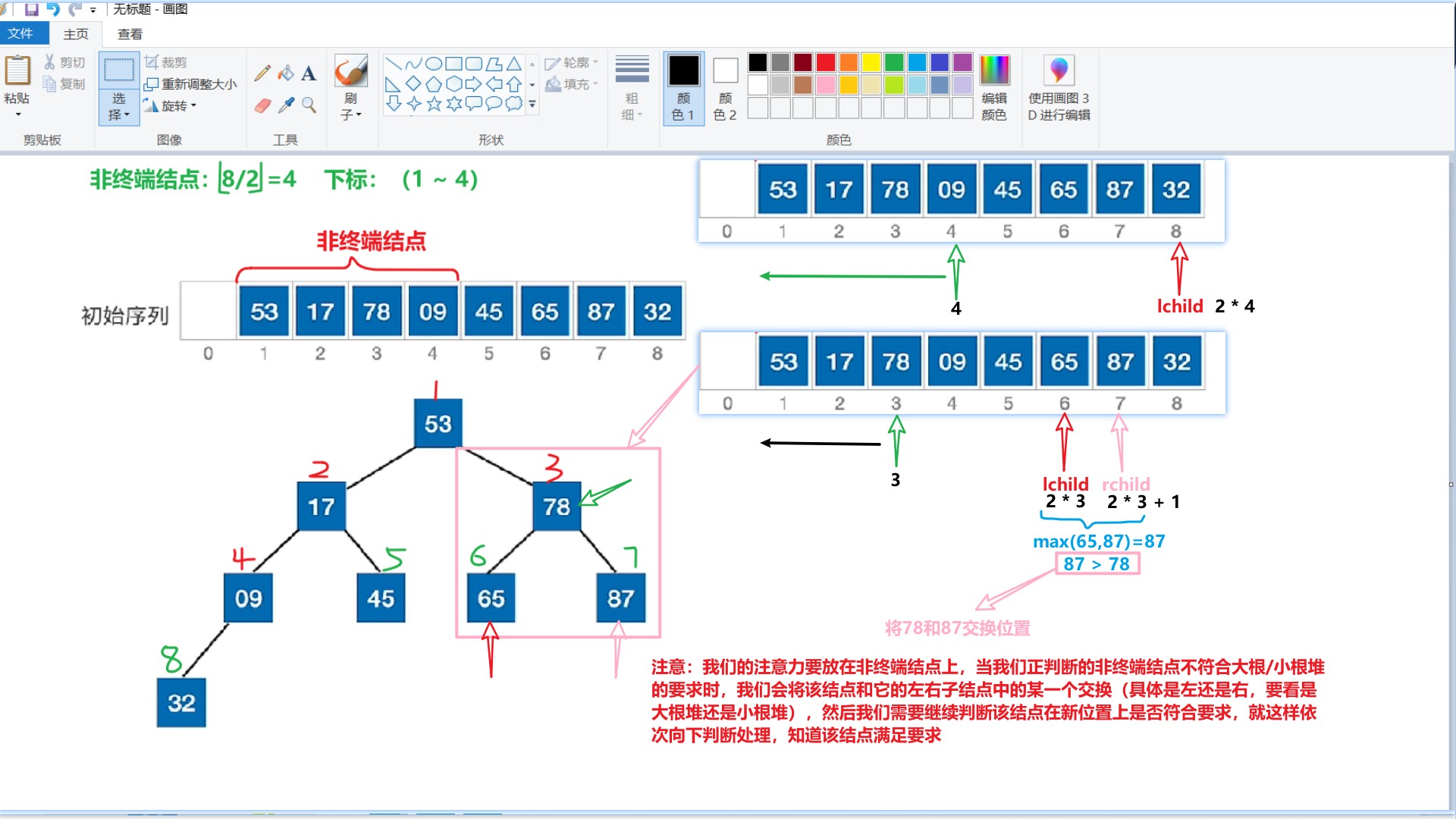
堆排序代码：

#include<iostream>
#include<vector>
using namespace std;//大根堆 
void HeadAdjust(vector<int> &v, int k, int len) {//将元素k为根的子树进行调整 
	for(int i = 2 * k; i <= len; i *= 2) {
		if(i + 1 <= len && v[i] < v[i + 1]) {
		//这里的i+1<=len是为了保证v[i+1]有意义，即该子树有右孩子 
		//v[i]<v[i + 1]表明子树的右孩子大于左孩子，所以要将i指向子树的右孩子
			i++;//因为i指向的是子树的左孩子，i++就将i指向子树的右孩子了	
		}//如果没有进入这个if语句，那么此时的i仍指向的是子树的左孩子 
		//综上所述，到步后i所指向的是该子树左右孩子中较大的那一个 
		if(v[k] >= v[i]) {//根结点更大无须调整 
			break; 
		}else {//不满足根结点更大的要求，需要调整
			v[0] = v[k];//暂存子树的根结点
			v[k] = v[i];
			v[i] = v[0]; 
			k = i;//修改k值，继续向下筛选
		} 
	}
}
void BuildMaxHeap(vector<int> &v) {
	int len = v.size() - 1;//这里的len其实就是最后一个元素的下标，注意是从v[1]开始存的 
	for(int i = len / 2; i >= 1; i--) {
		HeadAdjust(v, i, len);
	}
}
void HeapSort(vector<int> &v) {
	int len = v.size() - 1;
	BuildMaxHeap(v);
	for(int i = len; i > 1; i--) {
		swap(v[i], v[1]);//将堆顶元素和堆底元素交换
		HeadAdjust(v, 1, i - 1); //把剩余的i-1个元素整理成堆 
	} 
}
int main() {
	int n;
	cout << "请输入待排序序列中元素的个数：";
	cin >> n;
	vector<int> v(n + 1);
	cout << "请输入待排序序列：";
	for(int i = 1; i <= n; i++) {
		cin >> v[i];
	} 
	HeapSort(v);
	for(int i = 1; i <= n; i++) {
		cout << v[i] << " ";
	} 
	return 0;
} 

插入元素：对堆进行插入操作时，先将新结点放在堆的末端，再对这个新结点向上执行调整操作，即依次向上与之父结点进行比较（上升操作）

删除元素：在进行删除操作时，我们会将堆底元素换到被删除元素的位置，然后让该元素不断下坠

在向有n个元素的堆中插入一个新元素时，需要调用一个向上调整的算法，比较次数最多等于树的高度减一，由于树的高度为

⌊ log2n ⌋ + 1,所以堆的向上调整算法的比较次数最多等于⌊ log2n ⌋。

归并排序：（稳定）

空间复杂度：Merge()操作中，辅助空间刚好为n个单元，所以算法的空间复杂度为O(n)

时间复杂度：每趟归并的时间复杂度为O(n),共需要log2n趟归并，所以算法的时间复杂度为O(nlog2n)

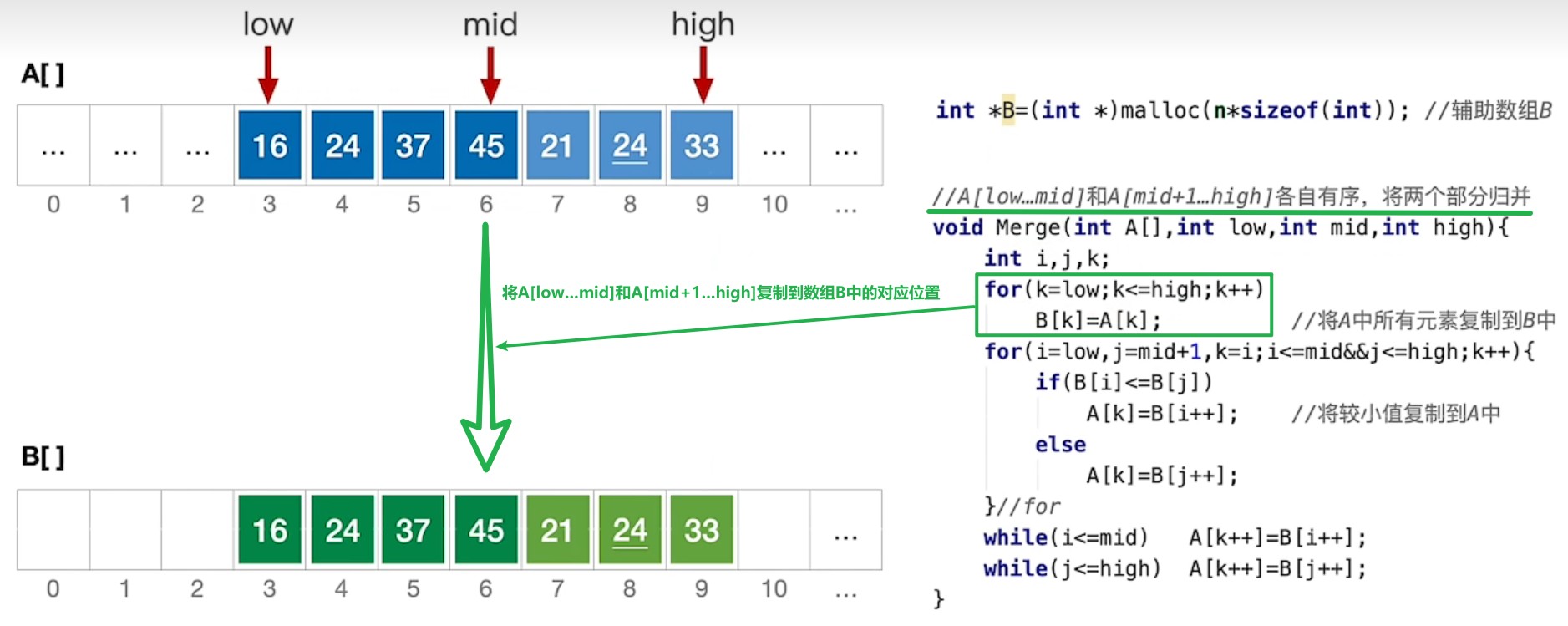
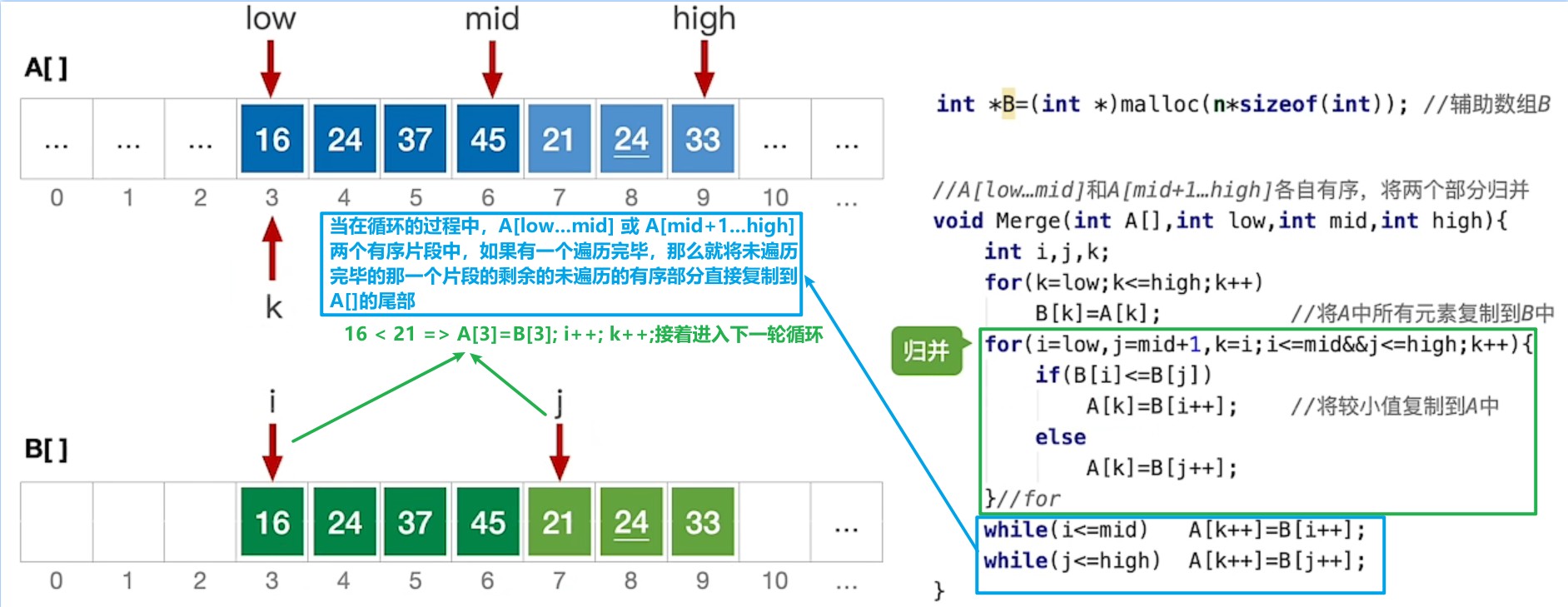
归并排序的一个核心步骤就是将两个有序的序列合并为一个有序的序列（2-路归并）

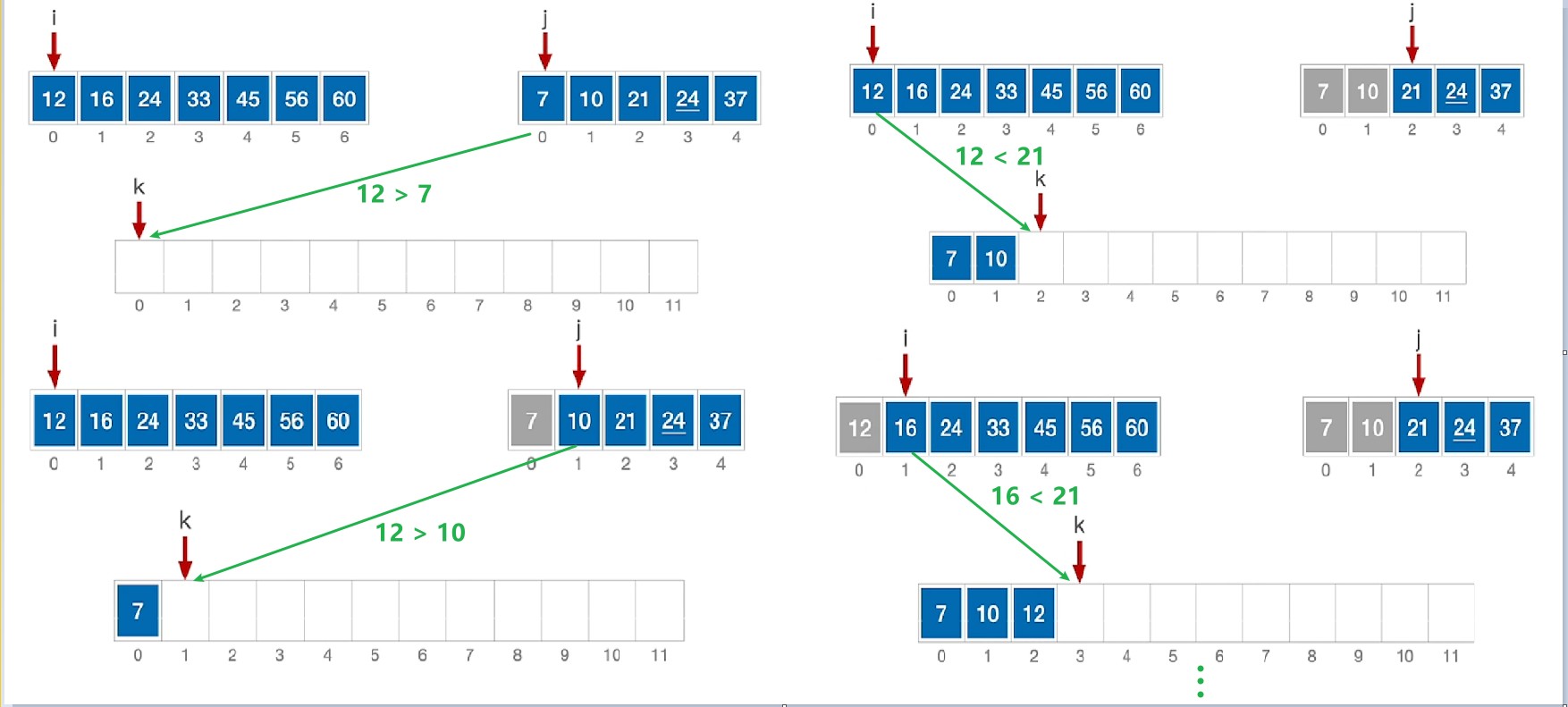
由此我们也可以推断出其他多路归并的情况

对于2路-归并排序，采用的是2路归并

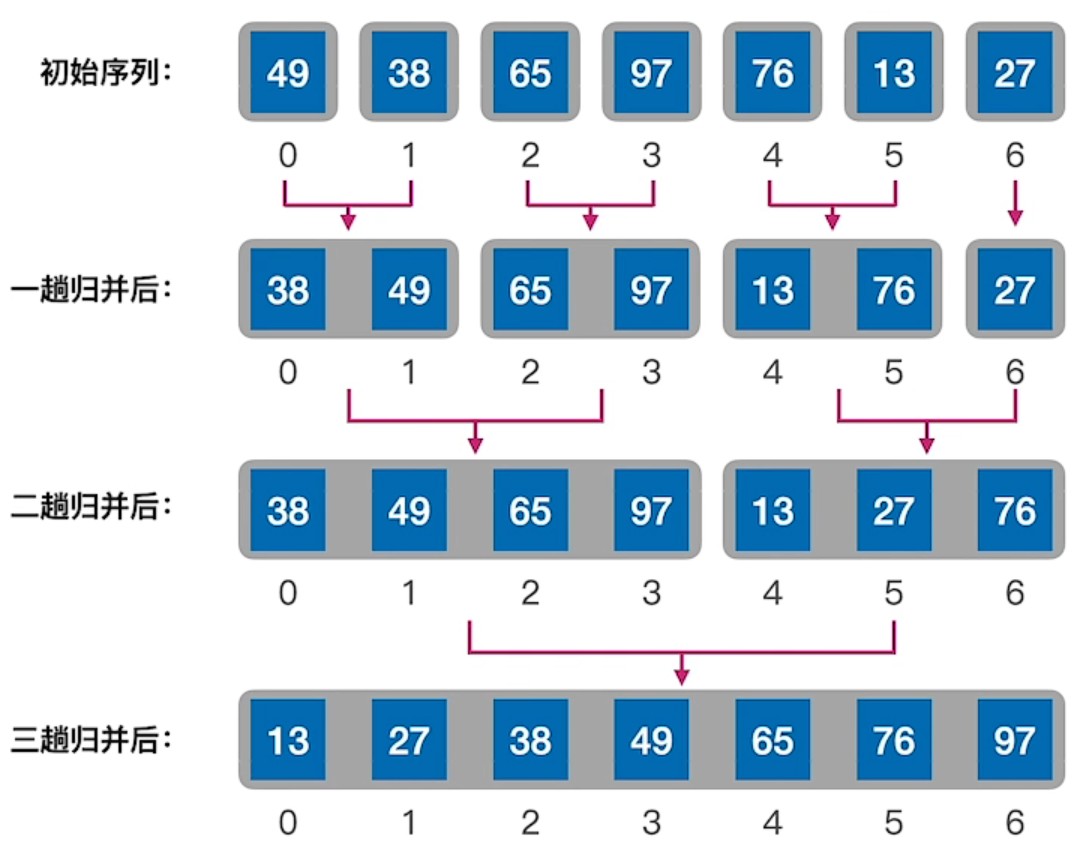
二路归并排序Merge归并部分具体代码的图文解析

#include<iostream>
#include<vector>
using namespace std;
void Merge(vector<int> &A, int low, int mid, int high) {
//A[low...mid]和A[mid+1...high]各自已经有序，现将这两个有序序列合并为一个有序序列 
	int i, j, k;
	vector<int> B(A.size());//辅助数组B 
	for(k = low; k <= high; k++) {
		B[k] = A[k];//将A中所有元素复制到B中 
	}
	for(i = low, j = mid + 1, k = i; i <= mid && j <= high; k++) {
		if(B[i] <= B[j]) {
			A[k] = B[i++];//将较小值复制到A中 
		}else {
			A[k] = B[j++];
		}
	}
	while(i <= mid) A[k++] = B[i++];
	while(j <= high) A[k++] = B[j++];
}
void MergeSort(vector<int> &A, int low, int high) {
	if(low < high) {
		int mid = (low + high) / 2;//从中间划分
		MergeSort(A, low, mid);//对左半部分归并排序
		MergeSort(A, mid + 1, high);//对右半部分归并排序
		Merge(A, low, mid, high);//归并
	}
} 
int main() {
	int n;
	cout << "请输入待排序序列中元素的个数："; 
	cin >> n;
	vector<int> A(n); 
	cout << "请输入待排序序列："; 
	for(int i = 0; i < n; i++) {
		cin >> A[i];
	}
	MergeSort(A, 0, n - 1);
	for(int i = 0; i < A.size(); i++) {
		cout << A[i] << " ";
	}
	return 0;
}

字符串匹配算法

KMP算法：

数据：1、待匹配的字符串（例如：googlogoogoogle） 2、模板字符串（例如：google）

思路：先通过模板字符串计算出next[]数组 (该例题的结果：next[] = {-1 0 0 0 1 0});然后通过这个next数组来在待匹配的字符串中 查找模板字符串的位置。（该例题的结果为：9）

优点：通过next[]数组来进行模板字符串的匹配，就可以减少很多不必要的字符比较，这样就大大的减少了算法所需要的时间

完整代码：

function get_next(next, t) {
            let j, k;
            let n = t.length;
            next[0] = -1;
            next[1] = 0;
            for (let i = 2; i < n; i++) {
                j = 1;
                k = 0;
                let tempj = j;
                while (tempj < i) {
                    if (t[tempj] == t[k]) {
                        tempj++;
                        k++;
                    } else {
                        j++;
                        tempj = j;
                        k = 0;
                    }
                }
                next[i] = k;
            }
        }

        function index_kmp(next, s, t) {
            let i = 0,
                j = 0;
            let s_n = s.length;
            let t_n = t.length;
            while (i < s_n && j < t_n) {
                if (j == -1 || s[i] == t[j]) {
                    j++;
                    i++;
                } else {
                    j = next[j];
                }
            }
            if (j >= t_n) {
                return i - t_n;
            } else {
                return -1;
            }
        }

next[]数组的求法：

按照如上方法先求出next数组，然后通过next数组来确定下一次匹配时j的位置。